At Polymathic-AI, part of our mission is to develop foundation models that help with scientific exploration and discovery. But it’s not enough to build these models, we also want to understand them! What algorithms do these networks actually learn under the hood? By uncovering them, we might discover improvements to our foundation models or even new insights about the scientific domains they represent.

To understand how Transformers solve complex problems, it helps to start with simpler tasks. In a recent paper, we do exactly this. We introduce a new toy problem designed to help us understand how Transformers can count in a context-dependent way—a core capability for scientific and quantitative reasoning. We call this task contextual counting. Contextual counting asks the model to count tokens in different regions of a sequence. As such, it idealizes scenarios where precise localization and subsequent computation are critical, such as counting specific neuro-receptors within a neuron in biological research. While seemingly simple, this task is surprisingly hard for state-of-the-art LLMs.

Introducing the Contextual Counting Task

In this task, the input is a sequence composed of zeros, ones, and square bracket delimiters: {0, 1, [, ]}. Each sample sequence contains ones and zeros with several regions marked by the delimiters. The task is to count the number of ones within each delimited region. For example, given the sequence:

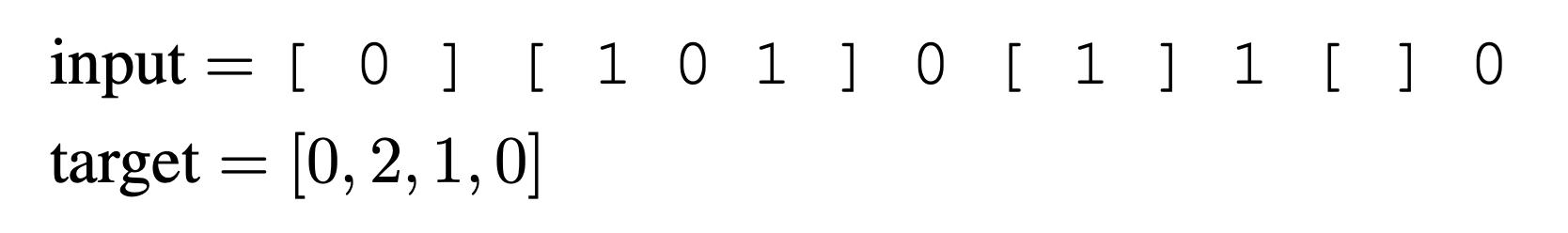
For simplicity, the regions are non-overlapping.

To tackle this task using a Transformer architecture, we use an encoder-decoder setup and provide the decoder with a fixed prompt that labels the regions. For the example above, the prompt would be:

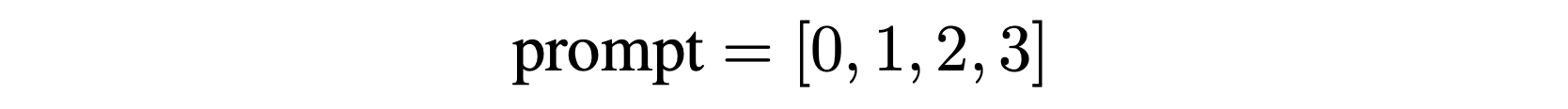
For our experiments, we fix the number of regions to 4 and the sequence length to 512. This allows us to explore how solutions generalize to different numbers of regions and sequence lengths.

Theoretical Insights

We provide some theoretical insights into the problem, showing that a Transformer with one causal encoding layer and one decoding layer can solve the contextual counting task for arbitrary sequence lengths and numbers of regions.

Contextual Position (CP)

Contextual position refers to positional information in a sequence that is meaningful only within the context of the problem. For the contextual counting task, this means knowing the region number for each token. For example, with three regions, the input and contextual positions might look like:

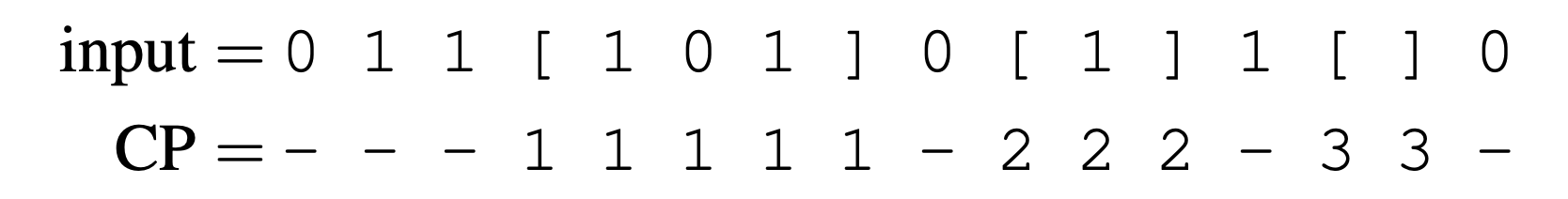
This information helps disambiguate the different regions based on context.

Key Propositions

• Proposition 1: If the regional contextual position information is available in the latent representation of the tokens at some layer of a Transformer, the contextual counting task can be solved with a single additional layer.
• Proposition 2: A causal Transformer with a single layer and no position encoding (NoPE) can infer the regional contextual position.

These propositions imply that a two-layer causal Transformer with NoPE can solve the contextual counting task.

Challenges for Non-Causal Transformers

For non-causal (bidirectional) Transformers, the task is more complicated:

• Proposition 3: A non-causal Transformer with no position code and a permutation-invariant output head cannot solve the contextual counting task.
• Proposition 4: To emulate a causal attention profile, a non-causal attention layer with Absolute Position code would need an embedding space at least as large as the sequence length.

These propositions highlight the difficulties non-causal Transformers face in solving this task.

Experimental Results

The theoretical results above imply that exact solutions exist but do not clarify whether or not such solutions can indeed be found when the model is trained via SGD. We therefore trained various Transformer architectures on this task. Inspired by the theoretical arguments, we use an encoder-decoder architecture, with one layer and one head for each. A typical output of the network is shown in the following image where the model outputs the probability distribution over the number of ones in each region.

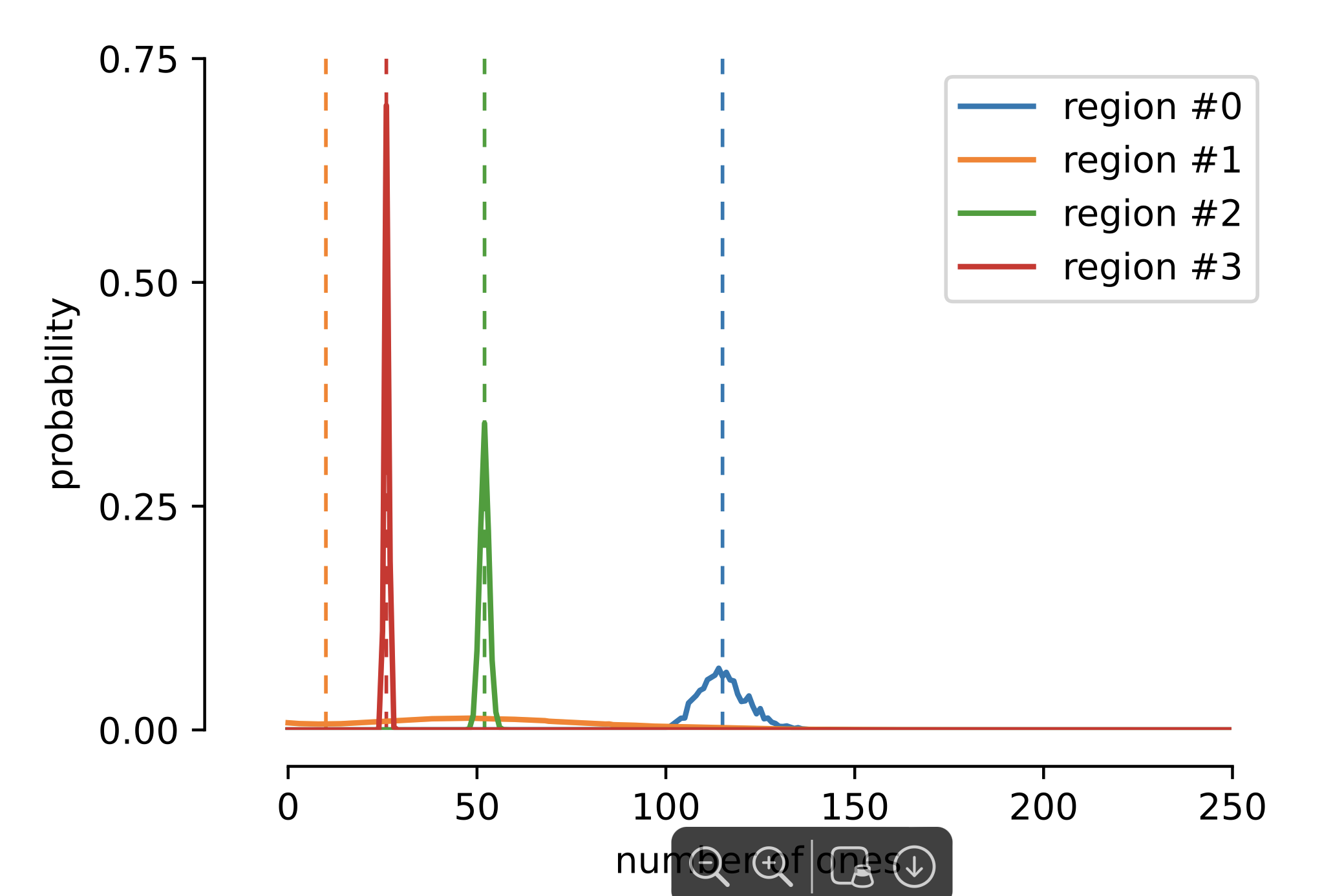
We summarize the results of this empirical exploration below.

1. Causal Transformers significantly outperform non-causal ones.

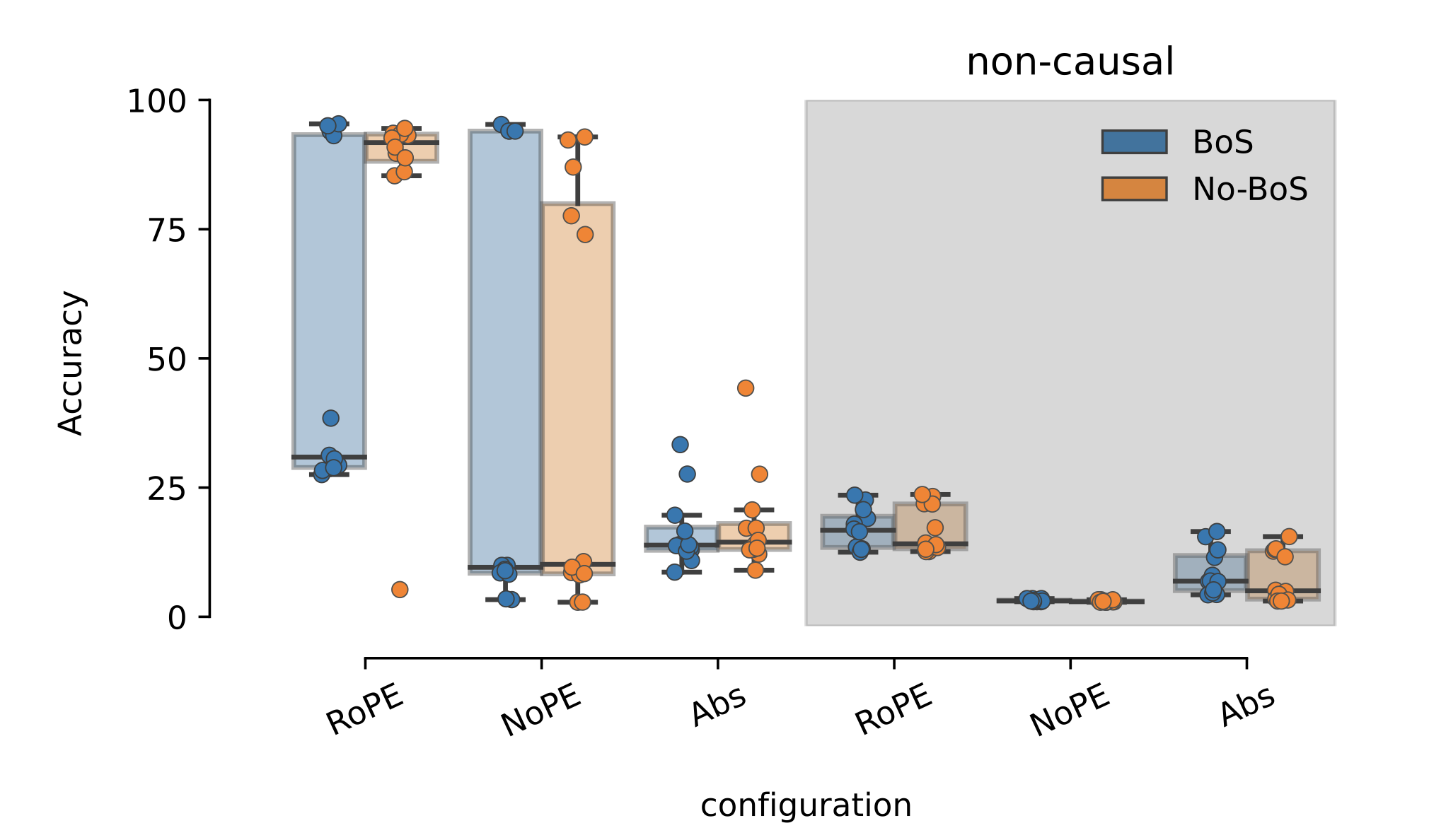
The above figure shows the performance of different Transformer configurations. The most prominent feature of this figure is that non-causal Transformers with any positional encoding fail to get good performance. In contrast, causal Transformers can achieve close to 100\% accuracy.

2. NoPE is best but harder to train than RoPE.

We also see that the very best model is trained with NoPE but RoPE is much more consistent in training.

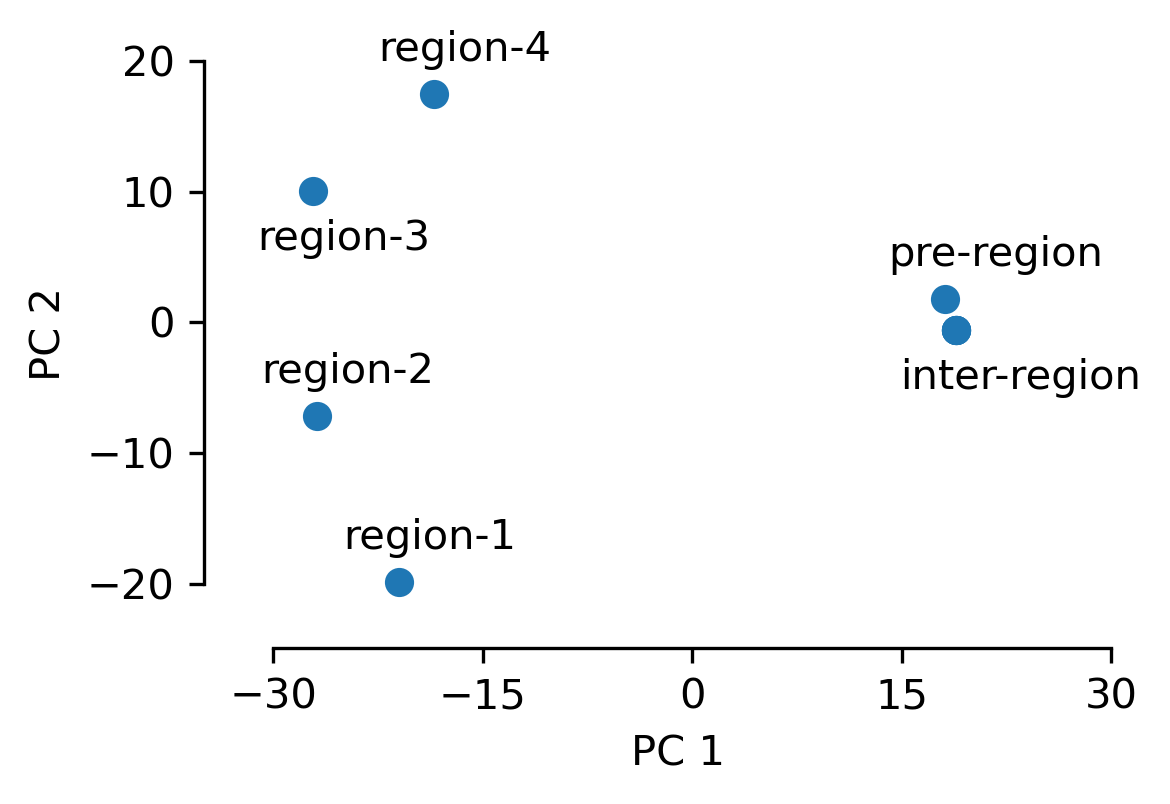
3. In the best performing models, the encoder captures the regional contextual position information.

As described above, the regional contextual position is an important piece of information for this task. Looking at the projection of the 1-token embeddings in the different regions, we see that this information is accurately captured.

By looking at the details of the attention module of the encoder, we see that in causal models, this information is inferred by attending to all the previous delimiter tokens equally. Each token can tell which region it is in by looking at how many delimiter tokens of each kind preceded it.

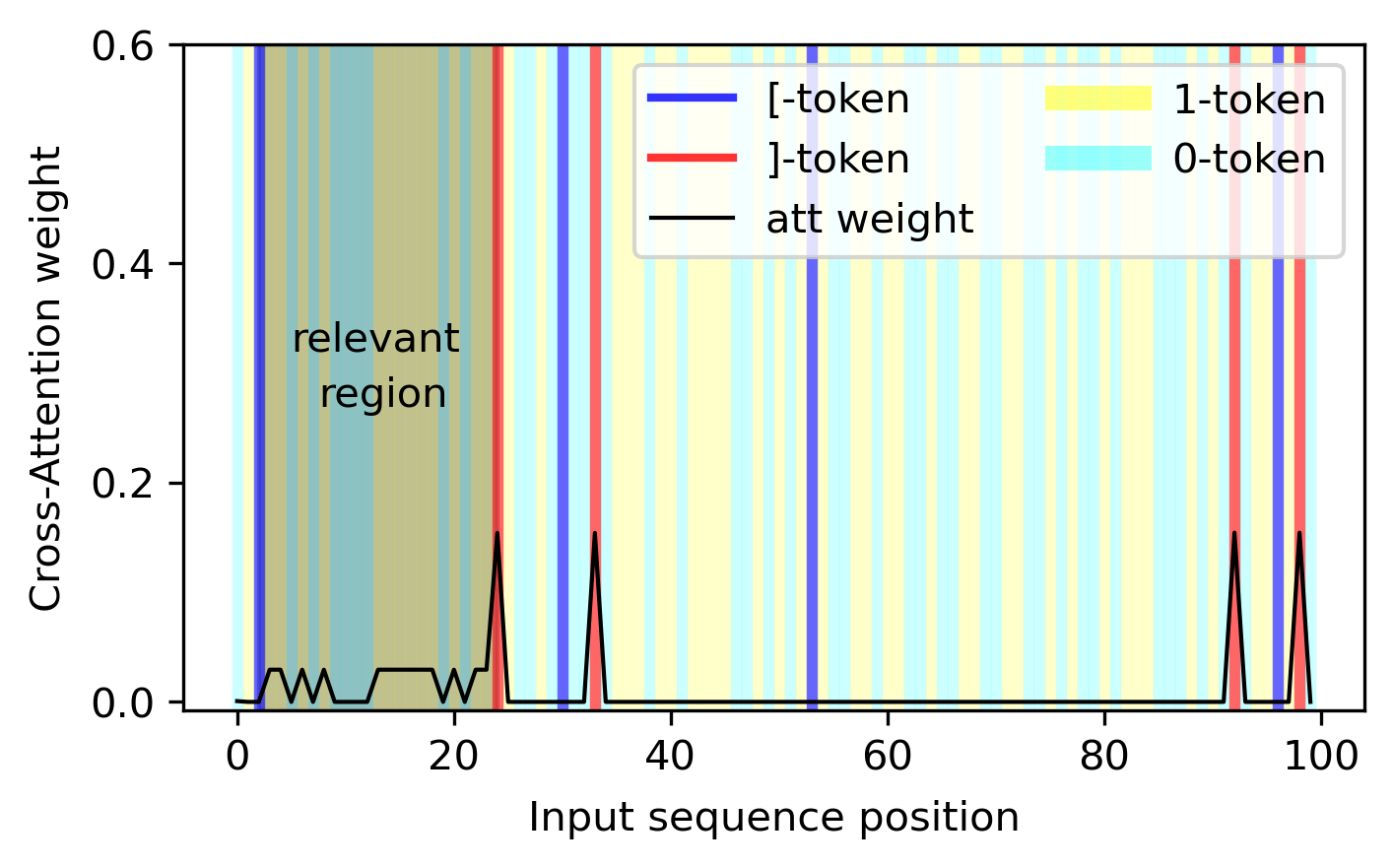
4. In the best performing models, the decoder attends only to the 1-tokens in the relevant region.

We can verify explicitly that the inferred regional contextual position in the encoder is used in the decoder cross-attention module such that the attention profile is focused on the 1-tokens of the relevant region (in the below figure, the third region).

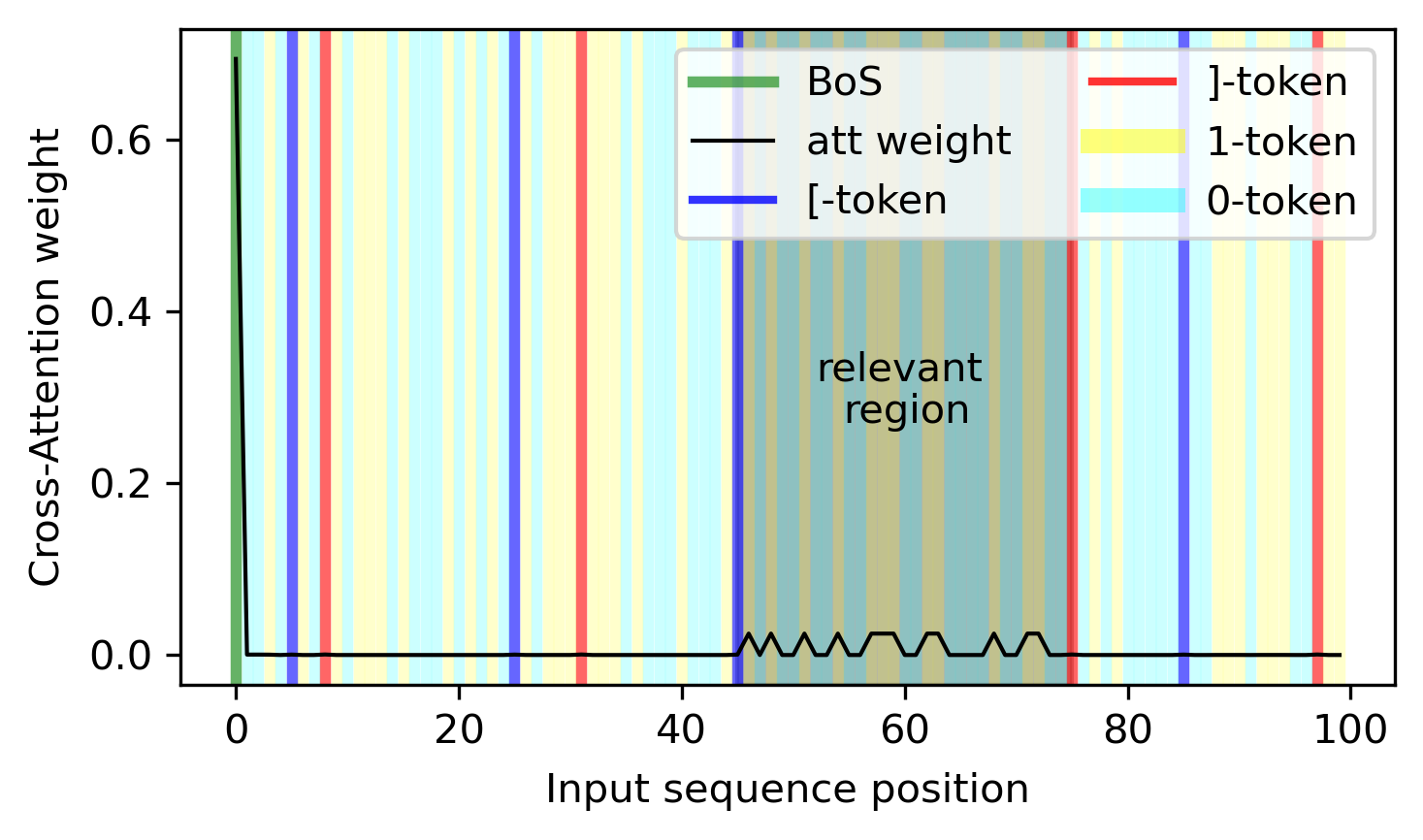
We see that in this example, the decoder also attends to the beginning-of-sequence token. The reason for this is that, if the model only attends to the 1-tokens, then the number of the 1-tokens - the quantity of interest - is going to cancel in the calculation of the softmax. However, if there is another token, then the number of 1-tokens will be preserved. In this way, this other token acts as a bias term when computing the output of the attention module.

6. Out-of-distribution generalization is directly linked to which tokens are used as bias terms.

The figure below shows the behavior of three different type of solutions when generalizing to sequences of different lengths and inputs with different number of regions. Even though all three attain the same performance on the in-distribution data, their out-of-distribution performance is very different. Why is this the case?

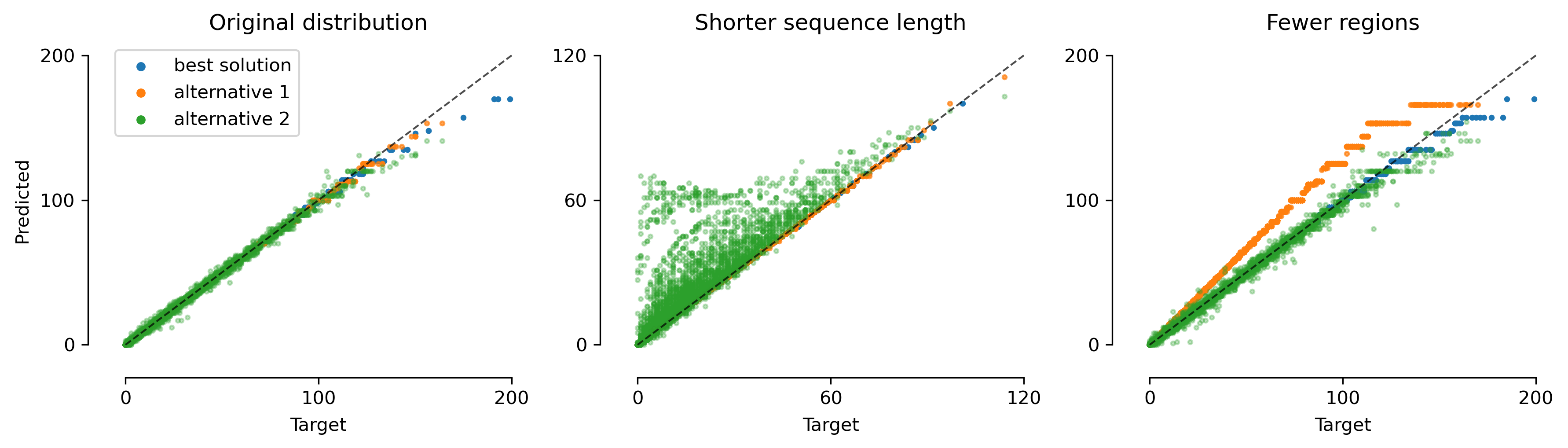
We can get a hint at what might be the culprit by looking at the attention pattern of the decoder. The attention pattern given in the previous point pertains to the blue dots on this figure, i.e. the model that generalizes best.

The figure below, shows the attention pattern of the orange dots, i.e. the model that generalizes do different sequence lengths but not to different region numbers. We see that as before, the decoder pays attention to the 1-tokens of the relevant region (in this case the first region), however this time the role of the bias term is played by the ]-tokens. During training, the number of regions is fixed at 4, and therefore the number of ]-tokens can be used as a constant bias. However, this is not the case when the number of regions changes. This explains why this model does not generalize to other number of regions.

In our exploration, we found that the model can use any combination of quantities that are constant during training as biases.

7. The network generates its output by balancing two learned shapes.

In some of our experiments, we chose to remove the MLP and self-attention layers from the decoder block. That is, the decoder is just a cross-attention layer. This configuration is less expressive but has the advantage that the output of the model is a linear combination of the value vectors derived from the embeddings of the encoder.

In a previous case we saw that the decoder only attended to the 1-tokens of the relevant region and the beginning-of-sequence token. The figure below shows the value vectors of these two tokens.

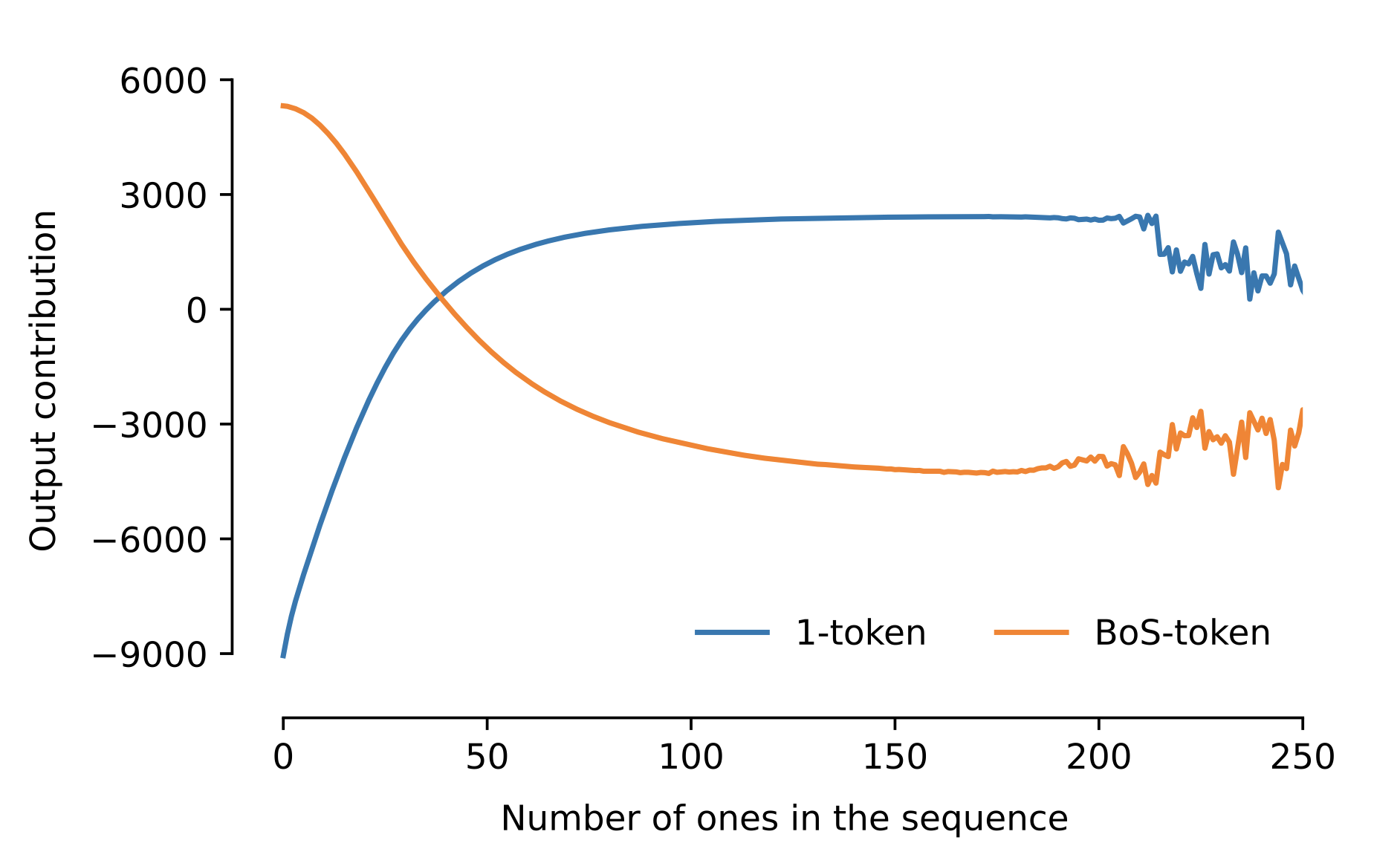
We can verify that by adding n-times the value vector of the 1-token to the value vector of the BoS-token, we arrive at a distribution that (after a softmax) is peaked at n. Comparing this with the output of the model, we see that this is indeed what the network is implementing.

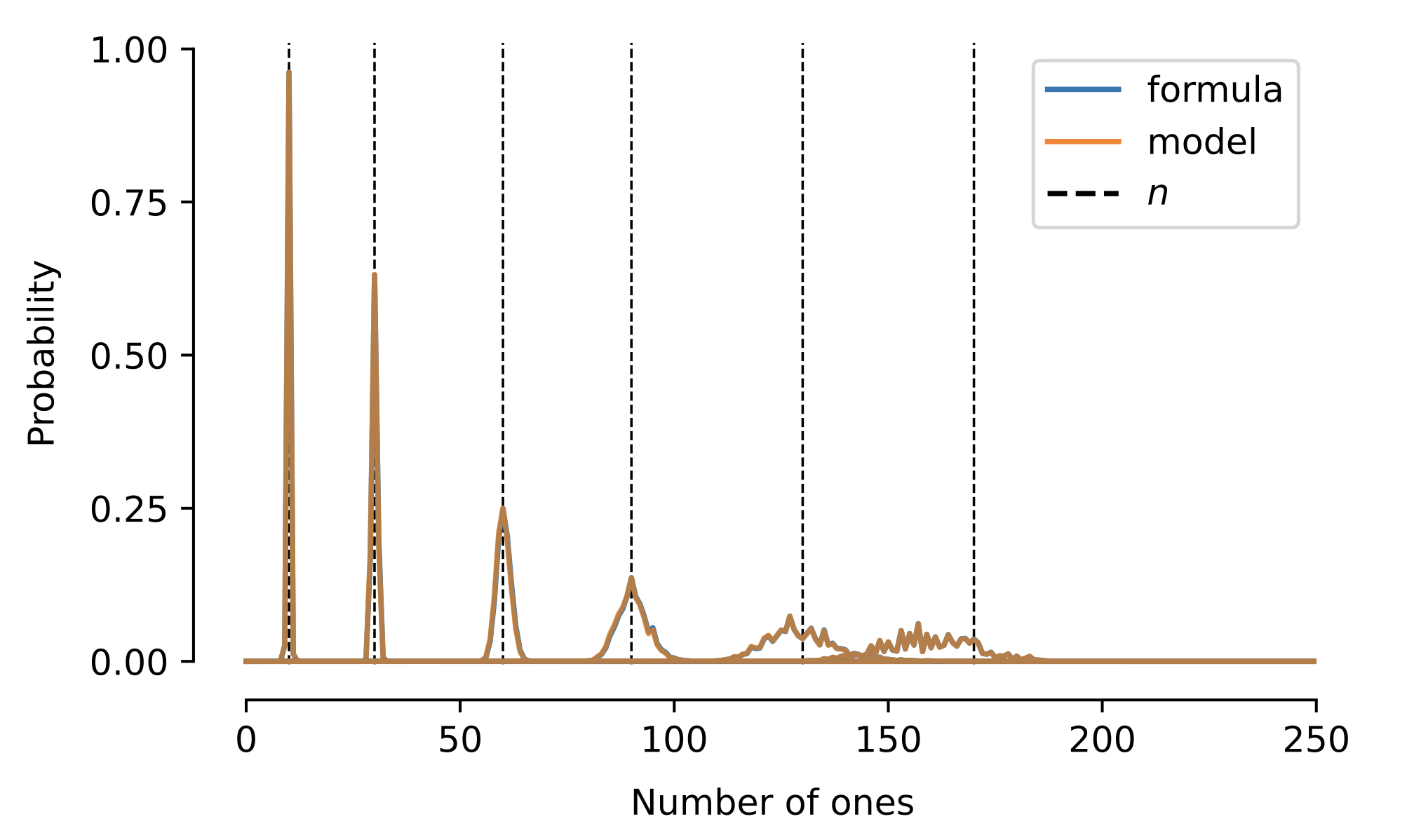
Therefore, in these models we fully understand what attention patterns the model is using, how these attention patterns are implemented and explicitly how the output of the network is constructed.

If you made it this far, here is an interesting bonus point:

• Even though the model has access to the number n through its attention profile, it still does not construct a probability distribution that is sharply peaked at n. As we see in the above figure, as n gets large, this probability distribution gets wider. This, we believe is partly the side-effect of this specific solution where two curves are being balanced against each other. But it is partly a general problem that as the number of tokens that are attended to gets large, we need higher accuracy to be able to infer n exactly. This is because the information about n is coded non-linearly after the attention layer. In this case, if we assume that the model attends to BoS and 1-tokens equally the output becomes:

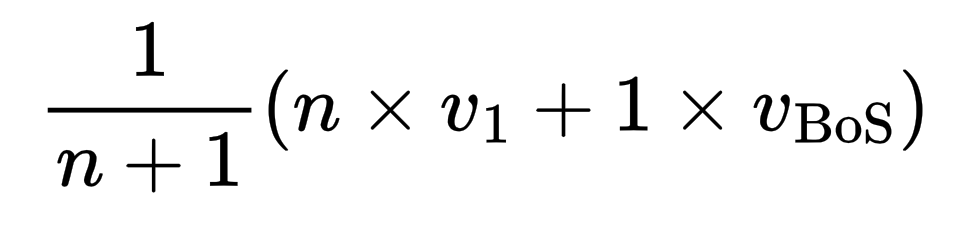
We see that as n becomes large, the difference between n and n+1 becomes smaller.

Conclusion

The contextual counting task provides a valuable framework for exploring the interpretability of Transformers in scientific and quantitative contexts. Our experiments show that causal Transformers with NoPE can effectively solve this task, while non-causal models struggle. These findings highlight the importance of task-specific interpretability challenges and the potential for developing more robust and generalizable models for scientific applications.

For more details, check out the paper.

– Siavash Golkar

Image by Tim Mossholder via Unsplash.