In recent years, the use of deep learning in science, particular in surrogate modeling, has exploded. Across the many scales of physics - from molecular dynamics to climate and weather and even up to cosmological scales - researchers have developed deep learning surrogates to accelerate their simulations. Right now, each of these surrogates is built from scratch. Learning new systems requires large datasets and larger training times every time researchers want to model new dynamics. This large upfront cost limits the accessibility of these methods for many physical systems of interest to the largest, most compute-rich organizations.

Does this need to be the case?

The fields of natural language processing and computer vision have been revolutionized by the emergence of “foundation models”. These are large neural networks that have been pretrained on massive datasets without the use of explicit labels. The remarkable thing about this approach is that access to these larger unlabeled datasets allows the models to learn broadly useful, generalizable features that are representative of shared patterns across the full domain. When researchers in these fields need to solve a new problem, they are able to fine-tune these models quickly and with less data because many intrinsic properties of the data distribution are already understood by the model. This improves both the accuracy and the accessibility of large-scale deep learning.

At a fundamental level, many physical systems also share underlying principles. Many of the equations describing physical behavior are derived from universal properties like conservation laws or invariances which persist across diverse disciplines like fluids, climate science, astrophysics, and chemistry. This surfaces when we look at individual disciplines. For example, the famed Navier-Stokes equations describing transport in viscous fluids can be derived up to several material assumptions from conservation of mass, momentum, and energy.

The success of pretraining in other fields and the existence of these shared principles gives rise to an interesting question:

Can we learn these shared features ahead of time through pretraining and accelerate the development of models for new physical systems?

Transfer learning is well-studied in the physical sciences, but to make it as applicable to the physical sciences as it is in vision and language today, we need to develop models that understand multiple types of physics. The more physics a model understands, the more fields can make use of its weights as an initialization for their own models.

Learning multiple physics in a single model is non-trivial. Unlike in vision and video where input channels represent pixel intensities, in physics, input channels represent entirely different fields with different behaviors which may vary both in behavior and scale depending on the physical system under study. In our work, we develop a pretraining approach that helps us avoid these issues and train a single model on diverse physical behavior.

Multiple Physics Pretraining

Our pretraining approach can be described in two steps:

1. Project the state variables from multiple physical systems into a shared normalized embedding space.
2. Train a single scalable transformer model to predict the next step of a spatiotemporal series based on a small number of snapshots describing the history.

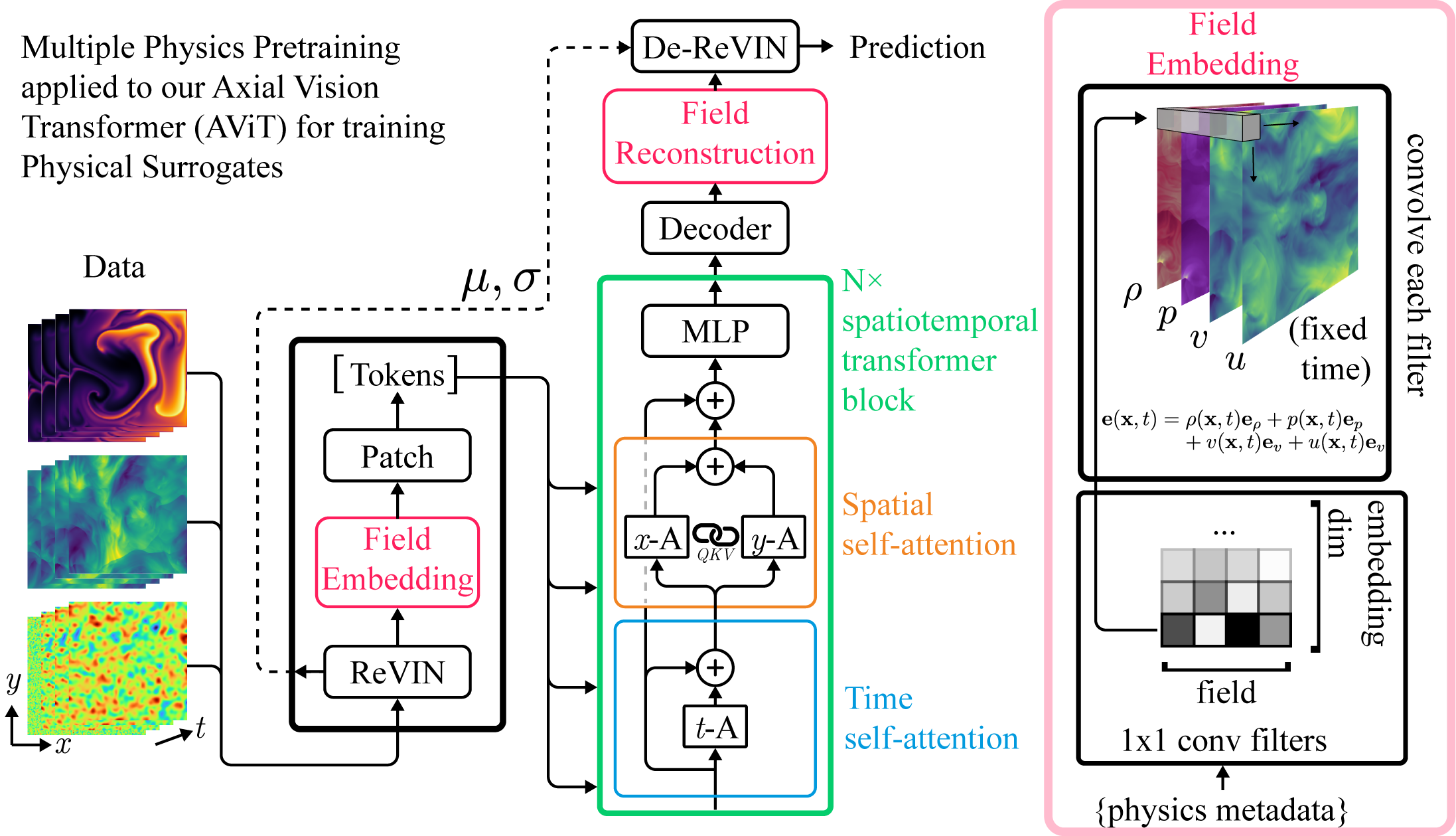
For step one, we first use a recent method from the time-series forecasting literature called Reversible Instance Normalization. This method unifies the scales of different datasets for ingestion into the network then re-injects the scale information back into the output. The normalized state variables are individually projected into a shared space with field-specific weights (right side of figure above).

From here, these can be processed by conventional transformers. However, we have a particular demand for scalability since many physical systems we are interested in are quite large. To minimize the computational load, we use an attention mechanism that looks only at one axis (time, height, width, ect) at a time to trade a bit of expressiveness for a significant computational savings.

Step two is essentially what is called “autoregressive pretraining” in the language literature. In language, until the recent emergence of chatbots, autoregressive language generation was seen as a convenient pretraining task. In surrogate modeling, autoregressive prediction is often our true objective. This makes it a natural approach to use over some of the other popular pretraining methods used in other fields.

Single Models can Simultaneously Learn Diverse Physics

We test out this strategy using a benchmark dataset called PDEBench. This dataset was developed for systems governed by partial differential equations (PDEs) with a significant emphasis on fluid mechanics.

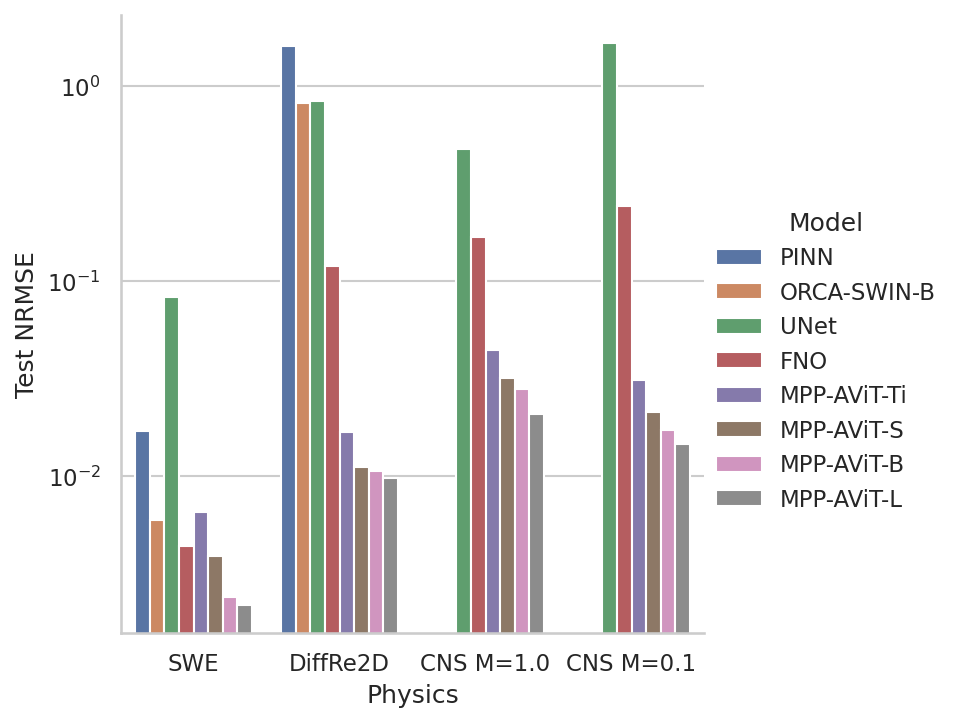
After pretraining, our models are able to compete with or beat modern baselines on all 2D time-dependent tasks in the benchmark despite the added difficulty of multi-task training. In fact, our multiple physics models outperform the similarly sized single-physics, dedicated baselines in a significant majority of cases and our results only improve with scale to the point where our largest models are the top performers across the board.

Learning Multiple Physics Transfers to New Systems

While this parity is impressive, we still expect fine-tuned, dedicated models to outperform general ones in most cases. The real question we would like to answer is whether this pretraining process actually improves the ability of the model to learn new physics. PDEBench has a natural division in the included fluid data between incompressible flow (Incompressible Navier-Stokes, Shallow Water) and compressible flow (Compressible Navier-Stokes). To explore the question, we pretrain new models without including compressible flow at all, then choose two distinct fine-tuning datasets. We call one “near” and the other “far”.

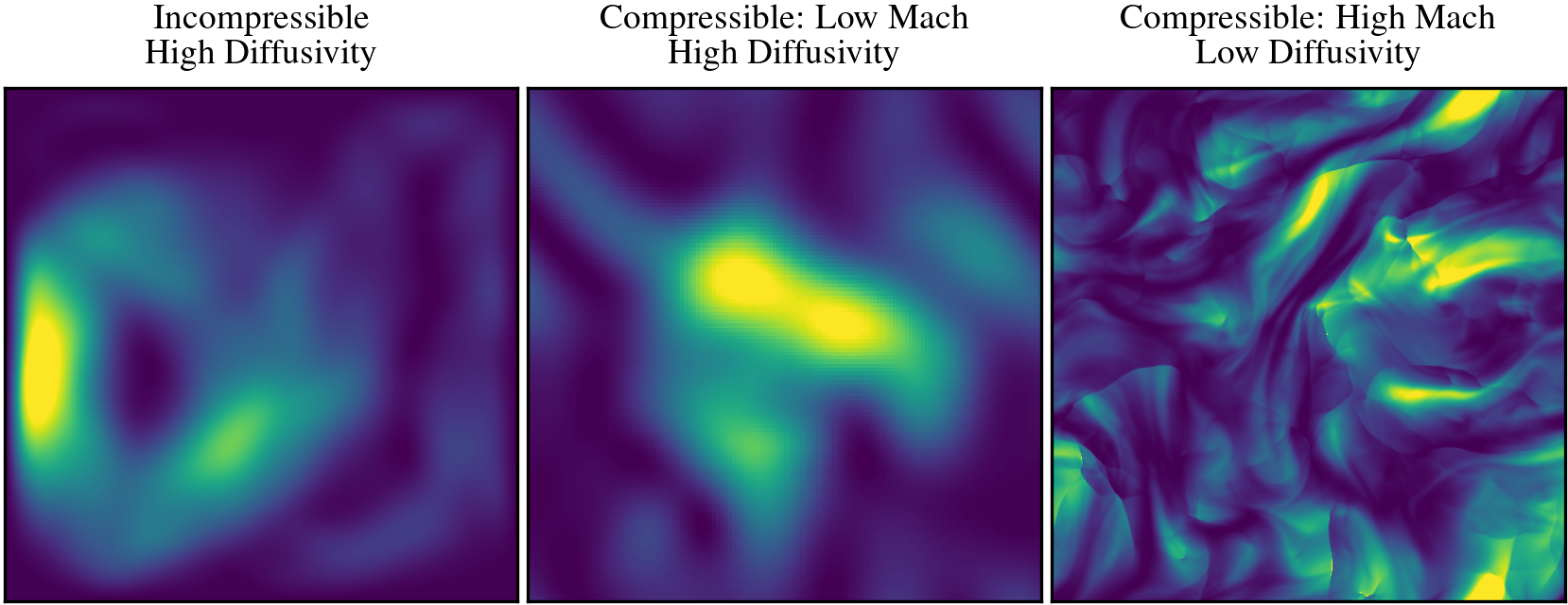
Both datasets are generated by a compressible flow solver, but while “near” (center) is selected to be physically very similar to the incompressible Navier-Stokes data in the training set (left), “far” (right) is generated in a different flow regime that exhibits wildly different behavior across scales. In both cases, there are still significant differences in the solver, resolution, and boundary conditions making both challenging transfer tasks.

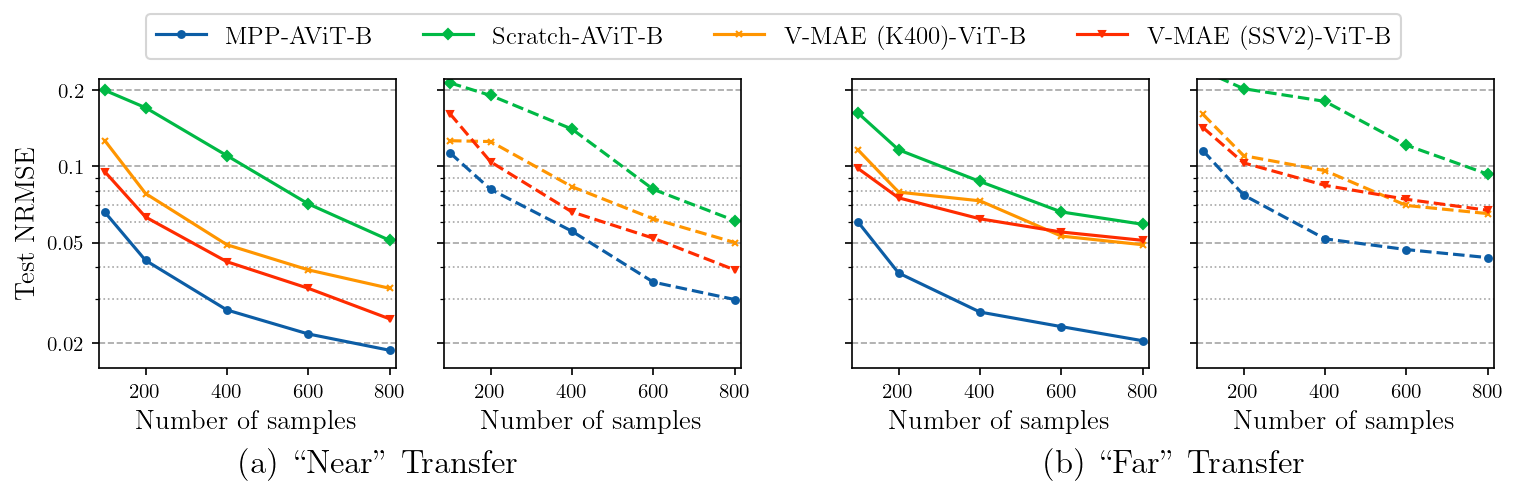
We’re trying to develop approaches that are applicable to domains where data generation is difficult or expensive, so we explore performance with different amounts of fine-tuning data. Fine-tuning from MPP (blue) outperforms both training from scratch (green) and fine-tuning from available pretrained spatiotemporal (video) models (red/yellow) across the full range of fine-tuning data both at one step (solid lines) and over multiple-step (5, dashed lines) rollouts.

Here’s an example of the long-term rollout after fine-tuning on only one-step-ahead prediction:

We can see numerical diffusion in the spectrum, but the model was trained on underresolved simulations so it would be surprising if we didn’t. Apart from that, the physical behavior is largely plausible. Boundary conditions are respected and the flow seems to be largely continuous. It is imperfect, but very promising.

Next Steps

Our work so far is still limited by the resolution and diversity of the training data. While datasets like PDEBench are valuable tools for exploration, creating true foundation models for general physics or even just fluids is going to require broader, deeper datasets capturing more behavior, trickier boundaries and geometries, and higher resolutions. There remains significant work to be done, but we’ve shown a new path forward by introducing a pretraining approach that allows us to train models that both learn multiple sets of physics simultaneously and effectively transfer to new physics.

For more information, check out our preprint on arXiv!

Title image by Ivan Bandura via Unsplash.