Acoustic Scattering - Inclusions¶
One line description of the data: Simple acoustic wave propogation over a domain split into two continuously varying sub-domains with a single discountinuous interface. With additive randomly generating inclusions (materials of significantly different density).
Longer description of the data: These variable-coefficient acoustic equations describe the propogation of an acoustic pressure wave through domains consisting of multiple materials with different scattering properties. This problem emerges in source optimization and it's inverse - that of identifying the material properties from the scattering of the wave - is a vital problem in geology and radar design. In this case, we have a variable number of initial point sources and a domain with random inclusions. These types of problems are of particular interest in geology where the inverse scattering is used to identify mineral deposits.
Domain expert: Michael McCabe, Polymathic AI.
Code or software used to generate the data: Clawpack, adapted from: this example.
Equation:
with \(\rho\) the material density, \(u, v\) the velocity in the \(x, y\) directions respectively, \(p\) the pressure, and \(K\) the bulk modulus.
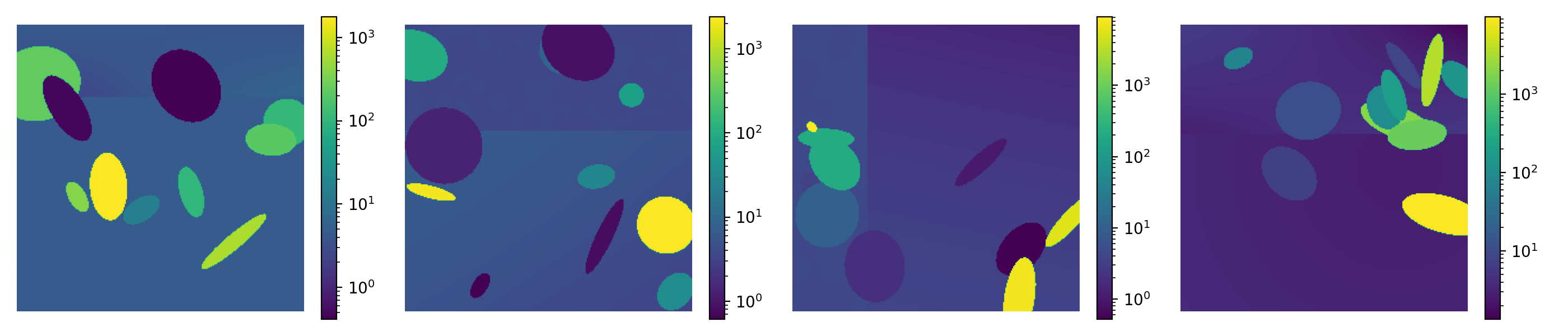
Example material densities can be seen below:
About the data¶
Dimension of discretized data: 101 steps of 256 \(\times\) 256 images.
Fields available in the data: pressure (scalar field), material density (constant scalar field), material speed of sound (constant scalar field), velocity field (vector field).
Number of trajectories: 4000.
Estimated size of the ensemble of all simulations: 283.8 GB.
Grid type: uniform, cartesian coordinates.
Initial conditions: Flat pressure static field with 1-4 high pressure rings randomly placed in domain. The rings are defined with variable intensity \(\sim \mathcal U(.5, 2)\) and radius \(\sim \mathcal U(.06, .15)\).
Boundary conditions: Open domain in \(y\), reflective walls in \(x\).
Simulation time-step: Variable based on CFL with safety factor .25.
Data are stored separated by (\(\Delta t\)): 2/101.
Total time range (\(t_{min}\) to \(t_{max}\)): [0, 2.].
Spatial domain size (\(L_x\), \(L_y\)): [-1, 1] x [-1, 1].
Set of coefficients or non-dimensional parameters evaluated:
-
\(K\) is fixed at 4.0.
-
\(\rho\) is the primary coefficient here. This is a superset of the single discontinuity example so the background is first generated two splits with one of the following distributions:
- Gaussian Bump - Peak density samples from \(\sim\mathcal U(1, 7)\) and \(\sigma \sim\mathcal U(.1, 5)\) with the center of the bump uniformly sampled from the extent of the subdomain.
- Linear gradient - Four corners sampled with \(\rho \sim \mathcal U(1, 7)\). Inner density is bilinearly interpolated.
- Constant - Constant \(\rho \sim\mathcal U(1, 7)\).
- Smoothed Gaussian Noise - Constant background sampled \(\rho \sim\mathcal U(1, 7)\) with IID standard normal noise applied. This is then smoothed by a Gaussian filter of varying sigma \(\sigma \sim\mathcal U(5, 10)\).
Inclusions are then added as 1-15 random ellipsoids with center uniformly sampled from the domain and height/width sampled uniformly from [.05, .6]. The ellipsoid is then rotated randomly with angle sampled [-45, 45]. For the inclusions, \(Ln(\rho)\sim \mathcal U(-1, 10)\).
Approximate time to generate the data: ~15 minutes per simulation.
Hardware used to generate the data and precision used for generating the data: 64 Intel Icelake cores per simulation. Generated in double precision.
What is interesting and challenging about the data:¶
Wave propogation through discontinuous media. Most existing machine learning datasets for computational physics are highly smooth and the acoustic challenges presented here offer challenging discontinuous scenarios that approximate complicated geometry through the variable density. The inclusions change wave propogation speed but only in small, irregular areas.
Please cite the associated paper if you use this data in your research:
@article{mandli2016clawpack,
title={Clawpack: building an open source ecosystem for solving hyperbolic PDEs},
author={Mandli, Kyle T and Ahmadia, Aron J and Berger, Marsha and Calhoun, Donna and George, David L and Hadjimichael, Yiannis and Ketcheson, David I and Lemoine, Grady I and LeVeque, Randall J},
journal={PeerJ Computer Science},
volume={2},
pages={e68},
year={2016},
publisher={PeerJ Inc.}
}