Euler Multi-quadrants - Riemann problems (compressible, inviscid fluid)

NOTE: this dataset is distributed in two separate datasets: euler_multi_quadrants_openBC with open boundary conditions and euler_multi_quadrants_periodicBC with periodic boundary conditions.

One line description of the data: Evolution of different gases starting with piecewise constant initial data in quadrants.

Longer description of the data: The evolution can give rise to shocks, rarefaction waves, contact discontinuities, interaction with each other and domain walls.

Associated paper: Paper.

Domain experts: Marsha Berger(Flatiron Institute & NYU), Ruben Ohana (CCM, Flatiron Institute & Polymathic AI), Michael McCabe (Polymathic AI).

Code or software used to generate the data: Clawpack (AMRClaw).

Equation: Euler equations for a compressible gas:

\begin{align}
U_t + F(U)_x + G(U)_y &= 0 \nonumber\\
\textrm{where} \quad U = \begin{bmatrix} \rho \nonumber\\ \rho u \\ \rho v \\ e \end{bmatrix}, \quad F(U) = \begin{bmatrix} \rho u \\ \rho u^2 + p \\ \rho u v \\ u(e + p) \end{bmatrix},& \quad G(U) = \begin{bmatrix} \rho v \\ \rho u v \\ \rho v^2 + p \\ v(e + p) \end{bmatrix}, \quad \\ e = \frac{p}{(\gamma - 1)} + \frac{\rho (u^2 + v^2)}{2}&, \quad p = A\rho^{\gamma}. \nonumber
\end{align}

with \(\rho\) the density, \(u\) and \(v\) the \(x\) and \(y\) velocity components, \(e\) the energy, \(p\) the pressure, \(\gamma\) the gas constant, and \(A>0\) is a function of entropy.

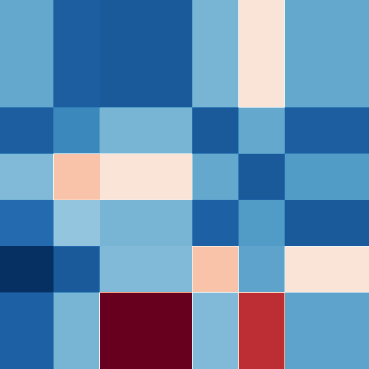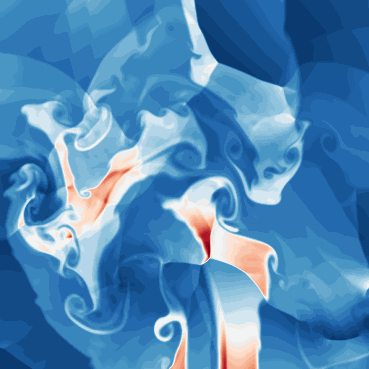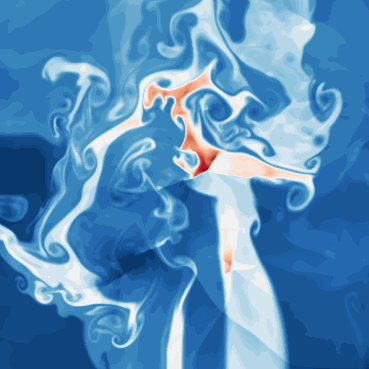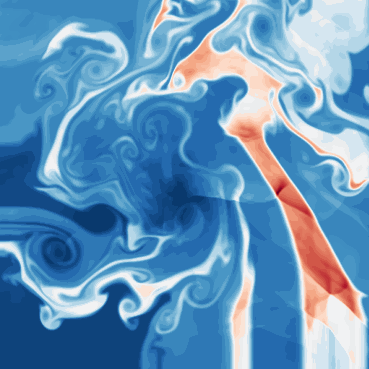
Dataset	FNO	TFNO	Unet	CNextU-net
euler_multi-quadrants_periodicBC	0.4081	0.4163	0.1834	\(\mathbf{0.1531}\)

Table: VRMSE metrics on test sets (lower is better). Best results are shown in bold. VRMSE is scaled such that predicting the mean value of the target field results in a score of 1.

About the data

Dimension of discretized data: 100 timesteps of 512x512 images.

Fields available in the data: density (scalar field), energy (scalar field), pressure (scalar field), momentum (vector field).

Number of trajectories: 500 per set of parameters, 10 000 in total.

Estimated size of the ensemble of all simulations: 5.17 TB.

Grid type: uniform, cartesian coordinates.

Initial conditions: Randomly generated initial quadrants.

Boundary conditions: Periodic or open.

Simulation time-step: variable.

Data are stored separated by (\(\Delta t\)): 0.015s (1.5s for 100 timesteps).

Total time range (\(t_{min}\) to \(t_{max}\)): \(t_{min} = 0\), \(t_{max}=1.5s\).

Spatial domain size (\(L_x\), \(L_y\)): \(L_x = 1\) and \(L_y = 1\).

Set of coefficients or non-dimensional parameters evaluated: all combinations of \(\gamma\) constant of the gas at a certain temperature: \(\gamma=\){1.13,1.22,1.3,1.33,1.365,1.4,1.404,1.453,1.597,1.76} and boundary conditions: {extrap, periodic}.

Approximate time to generate the data: 80 hours on 160 CPU cores for all data (periodic and open BC).

Hardware used to generate the data and precision used for generating the data: Icelake nodes, double precision.

What is interesting and challenging about the data:

What phenomena of physical interest are catpured in the data: capture the shock formations and interactions. Multiscale shocks.

How to evaluate a new simulator operating in this space: the new simulator should predict the shock at the right location and time, and the right shock strength, as compared to a pressure gauge monitoring the exact solution.

Please cite the associated paper if you use this data in your research:

@article{mandli2016clawpack,
  title={Clawpack: building an open source ecosystem for solving hyperbolic PDEs},
  author={Mandli, Kyle T and Ahmadia, Aron J and Berger, Marsha and Calhoun, Donna and George, David L and Hadjimichael, Yiannis and Ketcheson, David I and Lemoine, Grady I and LeVeque, Randall J},
  journal={PeerJ Computer Science},
  volume={2},
  pages={e68},
  year={2016},
  publisher={PeerJ Inc.}
}