Pattern formation in the Gray-Scott reaction-diffusion equations¶

One line description of the data: Stable Turing patterns emerge from randomness, with drastic qualitative differences in pattern dynamics depending on the equation parameters.

Longer description of the data: The Gray-Scott equations are a set of coupled reaction-diffusion equations describing two chemical species, \(A\) and \(B\), whose concentrations vary in space and time. The two parameters \(f\) and \(k\) control the “feed” and “kill” rates in the reaction. A zoo of qualitatively different static and dynamic patterns in the solutions are possible depending on these two parameters. There is a rich landscape of pattern formation hidden in these equations.

Associated paper: None.

Domain expert: Daniel Fortunato, CCM and CCB, Flatiron Institute.

Code or software used to generate the data: Github repository (MATLAB R2023a, using the stiff PDE integrator implemented in Chebfun. The Fourier spectral method is used in space (with nonlinear terms evaluated pseudospectrally), and the exponential time-differencing fourth-order Runge-Kutta scheme (ETDRK4) is used in time.)

Equation describing the data

\begin{align*}
\frac{\partial A}{\partial t} &= \delta_A\Delta A - AB^2 + f(1-A) \\ \frac{\partial B}{\partial t} &= \delta_B\Delta B - AB^2 - (f+k)B
\end{align*}

The dimensionless parameters describing the behavior are: \(f\) the rate at which \(A\) is replenished (feed rate), \(k\) the rate at which \(B\) is removed from the system, and \(\delta_A, \delta_B\) the diffusion coefficients of both species.

Gif

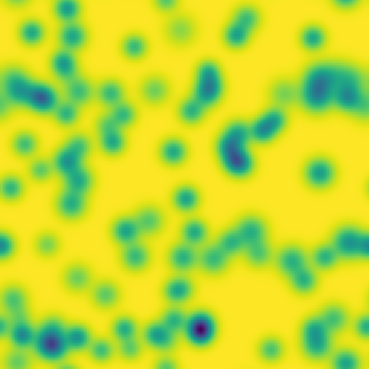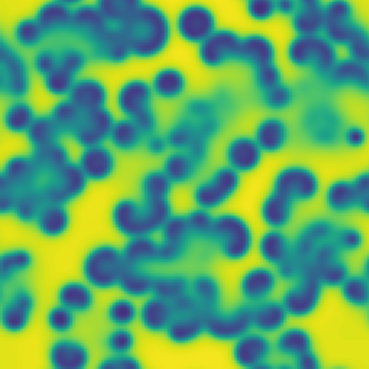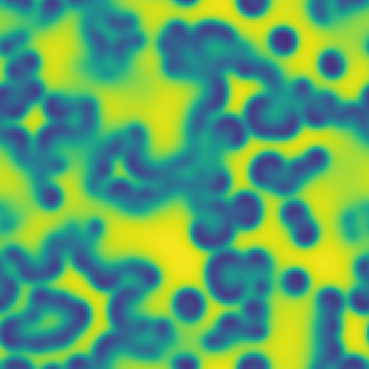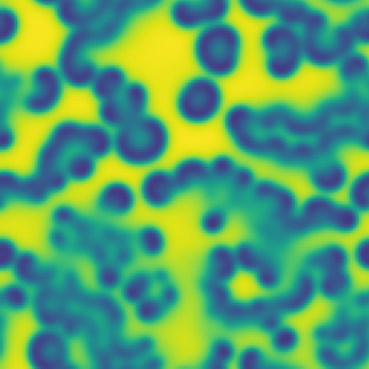
Dataset	FNO	TFNO	Unet	CNextU-net
`gray_scott_reaction_diffusion`	\(\mathbf{0.1365}\)	0.3633	0.2252	\(\mathbf{0.1761}\)

Table: VRMSE metrics on test sets (lower is better). Best results are shown in bold. VRMSE is scaled such that predicting the mean value of the target field results in a score of 1.

About the data¶

Dimension of discretized data: 1001 time-steps of 128 \(\times\) 128 images.

Fields available in the data: The concentration of two chemical species \(A\) and \(B\).

Number of trajectories: 6 sets of parameters, 200 initial conditions per set = 1200.

Estimated size of the ensemble of all simulations: 153.8 GB.

Grid type: uniform, cartesian coordinates.

Initial conditions: Two types of initial conditions generated: random Fourier series and random clusters of Gaussians.

Boundary conditions: periodic.

Simulation time-step: 1 second.

Data are stored separated by (\(\Delta t\)): 10 seconds.

Total time range (\(t_{min}\) to \(t_{max}\)): \(t_{min} =0\), \(t_{max} = 10,000\).

Spatial domain size (\(L_x\), \(L_y\)): \([-1,1]\times[-1,1]\).

Set of coefficients or non-dimensional parameters evaluated: All simulations used \(\delta_u = 2.10^{-5}\) and \(\delta_v = 1.10^{-5}\). "Gliders": \(f = 0.014, k = 0.054\). "Bubbles": \(f = 0.098, k =0.057\). "Maze": \(f= 0.029, k = 0.057\). "Worms": \(f= 0.058, k = 0.065\). "Spirals": \(f=0.018, k = 0.051\). "Spots": \(f= 0.03, k=0.062\).

Approximate time to generate the data: 5.5 hours per set of parameters, 33 hours total.

Hardware used to generate the data: 40 CPU cores.

What is interesting and challenging about the data:¶

What phenomena of physical interest are catpured in the data: Pattern formation: by sweeping the two parameters \(f\) and \(k\), a multitude of steady and dynamic patterns can form from random initial conditions.

How to evaluate a new simulator operating in this space: It would be impressive if a simulator—trained only on some of the patterns produced by a subset of the \((f, k)\) parameter space—could perform well on an unseen set of parameter values \((f, k)\) that produce fundamentally different patterns. Stability for steady-state patterns over long rollout times would also be impressive.

Warning: Due to the nature of the problem and the possibility to reach an equilibrium for certain values of the kill and feed parameters, a constant stationary behavior can be reached. Here are the trajectories for which a stationary behavior was identified for specy \(A\) as well as the corresponding time at which it was reached: - Validation set: - \(f=0.014, k=0.054\) : - Trajectory 7, time = 123 - Trajectory 8, time = 125 - Trajectory 10, time = 123 - Trajectory 11, time = 125 - Trajectory 12, time = 121 - Trajectory 14, time = 121 - Trajectory 15, time = 129 - Trajectory 16, time = 124 - Trajectory 17, time = 122 - Trajectory 18, time = 121 - Trajectory 19, time = 155 - \(f=0.018, k=0.051\) : - Trajectory 14, time = 109

Training set:
- \(f=0.014,k=0.054\) :
  - Trajectory 81, time = 126
  - Trajectory 82, time = 126
  - Trajectory 83, time = 123
  - Trajectory 85, time = 123
  - Trajectory 86, time = 124
  - Trajectory 87, time = 127
  - Trajectory 88, time = 121
  - Trajectory 90, time = 123
  - Trajectory 91, time = 121
  - Trajectory 92, time = 126
  - Trajectory 93, time = 121
  - Trajectory 94, time = 126
  - Trajectory 95, time = 125
  - Trajectory 96, time = 123
  - Trajectory 97, time = 126
  - Trajectory 98, time = 121
  - Trajectory 99, time = 125
  - Trajectory 100, time = 126
  - Trajectory 101, time = 125
  - Trajectory 102, time = 159
  - Trajectory 103, time = 129
  - Trajectory 105, time = 125
  - Trajectory 107, time = 122
  - Trajectory 108, time = 126
  - Trajectory 110, time = 127
  - Trajectory 111, time = 122
  - Trajectory 112, time = 121
  - Trajectory 113, time = 122
  - Trajectory 114, time = 126
  - Trajectory 115, time = 126
  - Trajectory 116, time = 126
  - Trajectory 117, time = 122
  - Trajectory 118, time = 123
  - Trajectory 119, time = 123
  - Trajectory 120, time = 125
  - Trajectory 121, time = 126
  - Trajectory 122, time = 121
  - Trajectory 123, time = 122
  - Trajectory 125, time = 125
  - Trajectory 126, time = 127
  - Trajectory 127, time = 125
  - Trajectory 129, time = 125
  - Trajectory 130, time = 122
  - Trajectory 131, time = 125
  - Trajectory 132, time = 131
  - Trajectory 133, time = 126
  - Trajectory 134, time = 159
  - Trajectory 135, time = 121
  - Trajectory 136, time = 126
  - Trajectory 137, time = 125
  - Trajectory 138, time = 126
  - Trajectory 139, time = 123
  - Trajectory 140, time = 128
  - Trajectory 141, time = 126
  - Trajectory 142, time = 123
  - Trajectory 144, time = 122
  - Trajectory 145, time = 125
  - Trajectory 146, time = 123
  - Trajectory 147, time = 126
  - Trajectory 148, time = 121
  - Trajectory 149, time = 122
  - Trajectory 150, time = 125
  - Trajectory 151, time = 126
  - Trajectory 152, time = 152
  - Trajectory 153, time = 127
  - Trajectory 154, time = 122
  - Trajectory 155, time = 124
  - Trajectory 156, time = 122
  - Trajectory 158, time = 126
  - Trajectory 159, time = 121
- \(f=0.018,k=0.051\):
  - Trajectory 97, time = 109
  - Trajectory 134, time = 107
  - Trajectory 147, time = 109
  - Trajectory 153, time = 112
Test set:
- \(f=0.014,k=0.054\):
  - Trajectory 12, time = 127
  - Trajectory 13, time = 125
  - Trajectory 14, time = 123
  - Trajectory 15, time = 126
  - Trajectory 16, time = 126
  - Trajectory 17, time = 123
  - Trajectory 18, time = 128
  - Trajectory 19, time = 125
- \(f=0.018,k=0.051\):
  - Trajectory 11, time = 113